6. Intuitive Limits and Continuity

b. Intuitive Definitions

2. 2-Sided Limits and Continuity

Given a function, \(f(x)\), and a point, \(x=a\), we have defined

In principle, these three numbers could all be different or one or more might not even exist. However, there are special words to describe the situations when \(2\) or \(3\) of these three numbers are equal.

  • If \(\displaystyle \lim_{x\to a^-}f(x)=f(a)\), then we say the \(f(x)\) is continuous from the left.
  • If \(\displaystyle \lim_{x\to a^+}f(x)=f(a)\), then we say the \(f(x)\) is continuous from the right.
  • If \(\displaystyle \lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L\), then we say the (\(2\)-sided) limit exists and is equal to \(L\) and we write: \[ \lim_{x\to a}f(x)=L \]
  • If \(\displaystyle \lim_{x\to a^-}f(x) =\lim_{x\to a^+}f(x)=f(a)\), then we say \(f(x)\) is continuous. Equivalently: \[ \lim_{x\to a}f(x)=f(a) \]

If we just say limit, we mean the \(2\)-sided limit.

def_LR_contL.jpg
Continuous from the left
but not continuous.
def_LR_contR.jpg
Continuous from the right
but not continuous.
def_LR_2sided.jpg
\(2\)-sided limit exists
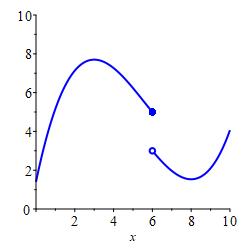
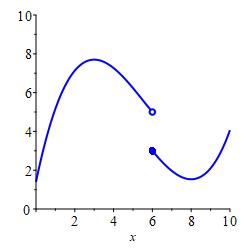
but not continuous.
def_LR_cont.jpg
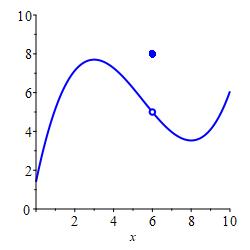
Continuous.

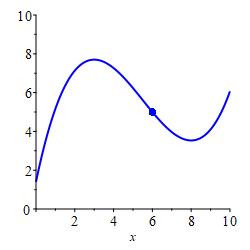
We say a (\(2\)-sided) limit is positive infinity if both the left and right limits are \(\infty\). We also say \(f(x)\) diverges to \(\infty\) and write: \[ \lim_{x\to a}f(x)=\infty \]

We say a (\(2\)-sided) limit is negative infinity if both the left and right limits are \(-\infty\). We also say \(f(x)\) diverges to \(-\infty\) and write: \[ \lim_{x\to a}f(x)=-\infty \]

def_2sided_inf.jpg
The limit does not exist but
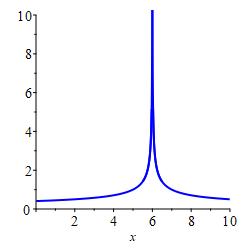
gets arbitrarily large and positive. \[ \lim_{x\to 6} f(x)=\infty \]
def_2sided_minf.jpg
The limit does not exist but
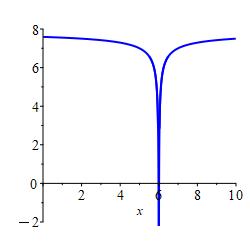
gets arbitrarily large and negative. \[ \lim_{x\to 6} f(x)=-\infty \]

To say a limit is \(\pm\infty\) does not say the limit exists, it merely says the way in which it diverges!

For the function plotted, compute each quantity or say Yes or No to each question.

From Exercise 2 on the previous page, we know: \[ \lim_{x\to 3^-}f(x)=4 \qquad \lim_{x\to 3^+}f(x)=2 \qquad f(3)=2 \]

ex_LR_lim.jpg
  1. Does the (\(2\)-sided) limit, \(\displaystyle \lim_{x\to 3}f(x)\), exist?

    The (\(2\)-sided) limit exists if the limits from the left and right exist and are equal: \[ \lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=L \] We then write: \[ \lim_{x\to 3}f(x)=L \]

    \(\displaystyle \lim_{x\to 3}f(x)\) does not exist because \(\displaystyle \lim_{x\to 3^-}f(x)=4\) while \(\displaystyle \lim_{x\to 3^+}f(x)=2\) which are not equal.

  2. If the (\(2\)-sided) limit exists, give its value. If it does not exist, enter infinity, -infinity or undefined.
    \(\displaystyle \lim_{x\to 3}f(x)=\,\)

    The (\(2\)-sided) limit exists if the limits from the left and right exist and are equal: \[ \lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=L \] We then write: \[ \lim_{x\to 3}f(x)=L \]

    \(\displaystyle \lim_{x\to 3}f(x)\) is undefined because it does not exist and it is neither \(\infty\) nor \(-\infty\).

  3. Is \(f(x)\) continuous from the left at \(x=3\)?

    \(f(x)\) is continuous from the left at \(x=3\) if \(\displaystyle \lim_{x\to 3^-}f(x)\) and \(f(3)\) exist and are equal: \[ \lim_{x\to 3^-}f(x)=f(3) \]

    \(f(x)\) is not continuous from the left at \(x=3\) because \(\displaystyle \lim_{x\to 3^-}f(x)=4\) while \(f(3)=2\) which are not equal.

  4. Is \(f(x)\) continuous from the right at \(x=3\)?

    \(f(x)\) is continuous from the right at \(x=3\) if \(\displaystyle \lim_{x\to 3^+}f(x)\) and \(f(3)\) exist and are equal: \[ \lim_{x\to 3^+}f(x)=f(3) \]

    \(f(x)\) is continuous from the right at \(x=3\) because \(\displaystyle \lim_{x\to 3^+}f(x)=f(3)=2\).

  5. Is \(f(x)\) continuous at \(x=3\)?

    \(f(x)\) is continuous at \(x=3\) if the limit from the left, the limit from the right and the value are all equal: \[ \lim_{x\to 3^-}f(x) =\lim_{x\to 3^+}f(x) =f(3) \]

    \(f(x)\) is not continuous at \(x=3\) because it is not continuous from the left.

For the piecewise function shown, compute each quantity or say Yes or No to each question.

From Exercise 3 on the previous page, we know: \[ \lim_{x\to 4^-}f(x)=2 \qquad \lim_{x\to 4^+}f(x)=3 \qquad f(4)=2 \]

\[ f(x)=\left\{ \begin{matrix} x-2 & \text{if} & x\lt4 \\ 2 & \text{if} & x=4 \\ x-1 & \text{if} & x\gt4 \end{matrix}\right. \]

  1. Does the (\(2\)-sided) limit, \(\displaystyle \lim_{x\to 4}f(x)\), exist?

    The (\(2\)-sided) limit exists if the limits from the left and right exist and are equal: \[ \lim_{x\to 4^-}f(x)=\lim_{x\to 4^+}f(x)=L \] We then write: \[ \lim_{x\to 4}f(x)=L \]

    \(\displaystyle \lim_{x\to 4}f(x)\) does not exist because \(\displaystyle \lim_{x\to 4^-}f(x)=2\) while \(\displaystyle \lim_{x\to 4^+}f(x)=3\) which are not equal.

  2. If the (\(2\)-sided) limit exists, give its value. If it does not exist, enter infinity, -infinity or undefined.
    \(\displaystyle \lim_{x\to 4}f(x)=\,\)

    The (\(2\)-sided) limit exists if the limits from the left and right exist and are equal: \[ \lim_{x\to 4^-}f(x)=\lim_{x\to 4^+}f(x)=L \] We then write: \[ \lim_{x\to 4}f(x)=L \]

    \(\displaystyle \lim_{x\to 4}f(x)\) is undefined because it does not exist and it is neither \(\infty\) nor \(-\infty\).

  3. Is \(f(x)\) continuous from the left at \(x=4\)?

    \(f(x)\) is continuous from the left at \(x=4\) if \(\displaystyle \lim_{x\to 4^-}f(x)\) and \(f(4)\) exist and are equal: \[ \lim_{x\to 4^-}f(x)=f(4) \]

    \(f(x)\) is continuous from the left at \(x=4\) because \(\displaystyle \lim_{x\to 4^-}f(x)=f(4)=2\).

  4. Is \(f(x)\) continuous from the right at \(x=4\)?

    \(f(x)\) is continuous from the right at \(x=4\) if \(\displaystyle \lim_{x\to 4^+}f(x)\) and \(f(4)\) exist and are equal: \[ \lim_{x\to 4^+}f(x)=f(4) \]

    \(f(x)\) is not continuous from the right at \(x=4\) because \(\displaystyle \lim_{x\to 4^+}f(x)=3\) while \(f(4)=2\) which are not equal.

  5. Is \(f(x)\) continuous at \(x=4\)?

    \(f(x)\) is continuous at \(x=4\) if the limit from the left, the limit from the right and the value are all equal: \[ \lim_{x\to 4^-}f(x) =\lim_{x\to 4^+}f(x) =f(4) \]

    \(f(x)\) is not continuous at \(x=4\) because it is not continuous from the right.

The following Maplets will help you identify the function value and the \(1\)-sided limits and help you determine whether the limit exists and whether the function is continuous from \(1\) or \(2\) sides (requires Maple on the computer where this is executed). The first two are equivalent to the tutorial on the next page.

Left and Right Limits and Continuity, given a Graph   Rate It

Left and Right Limits and Continuity, given a Formula   Rate It

Left and Right Limits and Continuity, given Numeric Data   Rate It

© MYMathApps

Supported in part by NSF Grant #1123255